“If there is a problem you can’t solve, then there is an easier problem you can solve: find it.” [George Pólya]
Abstract
Jeder, der Probleme strukturiert lösen möchte, sollte zunächst “Schule des Denkens” von George Pólya lesen.
Auch wenn Pólya hauptsächlich mathematische Probleme im Auge hatte, kann man seine Techniken allgemein anwenden.
Pólya’s Prinzipen
In seinem Buch unterscheidet Pólya 4 einfache Phasen des Problemlösens.
Wir wollen diese Phasen anhand einer Beispielaufgabe erläutern:
Beispiel:
Wandle eine Dezimalzahl mit Microsoft Excel in ihre Binärdarstellung um.
Phase 1 - Verstehen der Aufgabe
Zuerst müssen wir das Problem verstehen: Lesen und Umformulieren, Visualisieren.
Was ist gegeben, was gesucht?
Kann ich den Sachverhalt in eigenen Worten beschreiben?
Wie lautet die Bedingung?
Ist die Bedingung ausreichend, um die Unbekannte zu bestimmen?
Beispiel:
Gegeben ist eine beliebige Dezimalzahl. Gesucht ist deren Binärdarstellung in Excel. Diese Bedingung ist leider nicht ausreichend, im Allgemeinen die Unbekannte zu bestimmen.
Dies liegt einerseits an den Grenzen von Excel:
- Excel kann Dezimalzahlen lediglich mit einer Genauigkeit von 15 Stellen darstellen.
- Die kleinste negative darstellbare Dezimalzahl in Excel ist -2.2251E-308.
- Die kleinste positive darstellbare Dezimalzahl in Excel ist 2.2251E-308.
- Die größte negative darstellbare Dezimalzahl in Excel ist -9.99999999999999E+307.
- Die größte positive darstellbare Dezimalzahl in Excel ist 9.99999999999999E+307.
Diese Grenzen können wir deutlich erweitern, indem wir Dezimal- und Binärzahlen als Zeichenketten darstellen. Hier liegt Excel’s Grenze bei 32767 Zeichen pro Zelle. Dies lässt zwar immer noch keine allgemeine Lösung zu, sollte jedoch für alle praktisch vorkommenden Zahlen ausreichen.
Andererseits stoßen wir auch auf ein Darstellungsproblem:
Negative Zahlen werden im Binärsystem üblicherweise als Zweierkomplement dargestellt,
die führende Ziffer entspricht dem Vorzeichen (0 = positiv, 1 = negativ). Bei variabel langen
Nachkommastellen können wir kein Zweierkomplement berechnen.
Wir müssen also eine Fixkommadarstellung verwenden, oder wir beschränken die
Binärumwandlung im Falle von Nachkommastellen auf positive Zahlen. Das Gute ist:
Wir könnten wie bei Dezimalzahlen ein zusätzliches Vorzeichen (’+’ und ‘-’) einführen und
damit die Beschränkung aufheben.
Phase 2 - Ausdenken eines Planes
Der nächste Schritt besteht im Entwickeln eines Plans: Lösungswege und Definitionen wiederholen.
Für welche ähnlichen Probleme sind bereits Lösungen bekannt?
Kann das Problem in Teile zerlegt werden?
Welche Größen bleiben unverändert?
Stimmen die Maßeinheiten der Größen?
Wir gehen immer vom Gegebenen zum Gesuchten.
Beispiel:
Excel besitzt zwar eine eingebaute Funktion für die Umwandlung (DEZINBIN), aber diese Funktion ist auf ganze Zahlen von -512 bis +511 beschränkt, Nachkommastellen werden ignoriert.
Wir müssen also die Umrechnung von Dezimalzahlen in Zeichenkettendarstellung selbst implementieren. Bei der Implementierung helfen die Definitionen dieser benutzerdefinierten Funktionen:
- sbBinNeg - Ermittle das Zweierkomplement einer Binärzahl.
- sbDivBy2 - Teile eine positive Dezimalzahl durch 2.
- sbDecAdd - Addiere zwei positive Dezimalzahlen.
Phase 3 - Ausführen des Planes
Nun wird der Plan sorgfältig ausgeführt und anschaulich präsentiert.
Überprüfe jeden einzelnen Schritt.
Können wir jeden Schritt beweisen?
Ist unsere Lösungsbeschreibung anschaulich und verständlich?
Welche wichtigen Erkenntnisse haben wir gewonnen?
Beispiel:
Siehe die Implementierung sbDec2Bin im Anhang.
Phase 4 - Rückschau
Schließlich müssen wir unsere Lösung kritisch hinterfragen, bewerten und übertragen.
Können wir das Ergebnis überprüfen?
Können wir das Ergebnis auf andere (einfachere) Weise erreichen?
Können wir das Ergebnis oder die Problemlösungsmethode auf andere Probleme anwenden?
Haben wir das Problem vollständig gelöst?
Beispiel:
Wir stellen fest, dass bei periodischen Darstellungen im Binärsystem (z. B. besitzt die Dezimalzahl 0,1 keine endliche Binärdarstellung) und im Falle von notwendigem “Abschneiden” von Nachkommastellen aufgrund der Limitierung der Ziffern bei der Umwandlung von Nachkommastellen eine Ungenauigkeit nicht zu vermeiden ist.
Anmerkung: Der IEEE Standard 754 wurde eingeführt, um u. a. mit solchen Ungenauigkeiten umzugehen. Vollständig vermeiden lassen sie sich nicht.
Literatur
Pólya, George (2010). Schule des Denkens. A. Francke Verlag Tübingen und Basel. ISBN 978-3-7720-0608-1. Dies ist die deutsche Übersetzung seines englischen Titels How to Solve It.
Anhang
Wie lautet die binäre Darstellung (Bitlänge = 256) der Dezimalzahl -872362346234627834628734627834627834628? Die eingebaute Excel Funktion DEZINBIN hilft hier nicht weiter. Sie kann nur Eingaben von -512 bis 511 verarbeiten. Wenn Sie die korrekte Antwort
1111111111111111111111111111111111111111111111111111111111111111111111111111
1111111111111111111111111111111111111111111111111101011011111011010100011111
1001110111100101111001000010000111010110010010100110011010001001100111101010
0001010101001011110011111100
erhalten wollen, benutzen Sie bitte die unten gezeigte Funktion sbDec2Bin.
Bitte bachten: Nachkommastellen werden lediglich für positive Zahlen unterstützt. Zum Beispiel lautet die Dezimalzahl 0,5 im Binärformat 0,1.
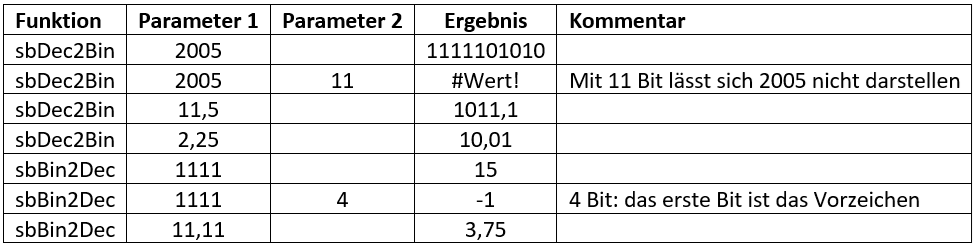
Programmcode sbDec2Bin
Bitte den Haftungsausschluss im Impressum beachten.
Option Explicit
Function sbDec2Bin(ByVal sDecimal As String, _
Optional lBits As Long = 32, _
Optional blZeroize As Boolean = False) As String
'Convert a decimal number into its binary equivalent.
'(C) (P) by Bernd Plumhoff 18-Dec-2021 PB V0.4
Dim sDec As String
Dim sFrac As String
Dim sD As String 'Internal temp variable to represent decimal
Dim sB As String
Dim blNeg As Boolean
Dim i As Long
Dim lPosDec As Long
Dim lLenBinInt As Long
lPosDec = InStr(sDecimal, Application.DecimalSeparator)
If lPosDec > 0 Then
If Left(sDecimal, 1) = "-" Then 'So far we cannot handle
'negative fractions
sbDec2Bin = CVErr(xlErrValue)
Exit Function
End If
sDec = Left(sDecimal, lPosDec - 1)
sFrac = Right(sDecimal, Len(sDecimal) - lPosDec)
lPosDec = Len(sFrac)
Else
sDec = sDecimal
sFrac = ""
End If
sB = ""
If Left(sDec, 1) = "-" Then
blNeg = True
sD = Right(sDec, Len(sDec) - 1)
Else
blNeg = False
sD = sDec
End If
Do While Len(sD) > 0
Select Case Right(sD, 1)
Case "0", "2", "4", "6", "8"
sB = "0" & sB
Case "1", "3", "5", "7", "9"
sB = "1" & sB
Case Else
sbDec2Bin = CVErr(xlErrValue)
Exit Function
End Select
sD = sbDivBy2(sD, True)
If sD = "0" Then
Exit Do
End If
Loop
If blNeg And sB <> "1" & String(lBits - 1, "0") Then
sB = sbBinNeg(sB, lBits)
End If
'Test whether string representation is in range and correct
'If not, the user has to increase lbits
lLenBinInt = Len(sB)
If lLenBinInt > lBits Then
sbDec2Bin = CVErr(xlErrNum)
Exit Function
Else
If (Len(sB) = lBits) And (Left(sB, 1) <> -blNeg & "") Then
sbDec2Bin = CVErr(xlErrNum)
Exit Function
End If
End If
If blZeroize Then sB = Right(String(lBits, "0") & sB, lBits)
If lPosDec > 0 And lLenBinInt + 1 < lBits Then
sB = sB & Application.DecimalSeparator
i = 1
Do While i + lLenBinInt < lBits
sFrac = sbDecAdd(sFrac, sFrac) 'Double fractional part
If Len(sFrac) > lPosDec Then
sB = sB & "1"
sFrac = Right(sFrac, lPosDec)
If sFrac = String(lPosDec, "0") Then
Exit Do
End If
Else
sB = sB & "0"
End If
i = i + 1
Loop
sbDec2Bin = sB
Else
sbDec2Bin = sB
End If
End Function
Programmcode sbBin2Dec
Bitte den Haftungsausschluss im Impressum beachten.
Function sbBin2Dec(sBinary As String, _
Optional lBits As Long = 32) As String
'Converts a binary number into its decimal equivalent.
'(C) (P) by Bernd Plumhoff 18-Dec-2021 PB V0.4
Dim sBin As String
Dim sB As String
Dim sFrac As String
Dim sD As String
Dim sR As String
Dim blNeg As Boolean
Dim i As Long
Dim lPosDec As Long
lPosDec = InStr(sBinary, Application.DecimalSeparator)
If lPosDec > 0 Then
If (Left(Right(String(lBits, "0") & sBinary, lBits), 1) = "1") And _
Len(sBin) >= lBits Then 'So far we cannot handle
'negative fractions
sbBin2Dec = CVErr(xlErrValue)
Exit Function
End If
sBin = Left(sBinary, lPosDec - 1)
sFrac = Right(sBinary, Len(sBinary) - lPosDec)
lPosDec = Len(sFrac)
Else
sBin = sBinary
sFrac = ""
End If
Select Case Sgn(Len(sBin) - lBits)
Case 1
sbBin2Dec = CVErr(xlErrNum)
Exit Function
Case 0
If Left(sBin, 1) = "1" Then
sB = sbBinNeg(sBin, lBits)
blNeg = True
Else
sB = sBin
blNeg = False
End If
Case -1
sB = sBin
blNeg = False
End Select
sD = "1"
sR = "0"
For i = Len(sB) To 1 Step -1
Select Case Mid(sB, i, 1)
Case "1"
sR = sbDecAdd(sR, sD)
Case "0"
'Do nothing
Case Else
sbBin2Dec = CVErr(xlErrNum)
Exit Function
End Select
sD = sbDecAdd(sD, sD) 'Double sd
Next i
If lPosDec > 0 Then 'now the fraction
sD = "0" & Application.DecimalSeparator & "5"
For i = 1 To lPosDec
If Mid(sFrac, i, 1) = "1" Then
sR = sbDecAdd(sR, sD)
End If
sD = sbDivBy2(sD, False)
Next i
End If
If blNeg Then
sbBin2Dec = "-" & sR
Else
sbBin2Dec = sR
End If
End Function
Programmcode sbDivBy2
Bitte den Haftungsausschluss im Impressum beachten.
Function sbDivBy2(sDecimal As String, blInt As Boolean) As String
'Divide positive sDecimal by two, blInt = TRUE returns integer only
'(C) (P) by Bernd Plumhoff 18-Dec-2021 PB V0.4
Dim i As Long
Dim lPosDec As Long
Dim sDec As String
Dim sD As String
Dim lCarry As Long
If Not blInt Then
lPosDec = InStr(sDecimal, Application.DecimalSeparator)
If lPosDec > 0 Then
sDec = Left(sDecimal, lPosDec - 1) & _
Right(sDecimal, Len(sDecimal) - lPosDec) 'Without decimal point
'lposdec already defines location of decimal point
Else
sDec = sDecimal
lPosDec = Len(sDec) + 1 'Location of decimal point
End If
If ((1 * Right(sDec, 1)) Mod 2) = 1 Then
sDec = sDec & "0" 'Append zero so that integer algorithm
'below calculates division exactly
End If
Else
sDec = sDecimal
End If
lCarry = 0
For i = 1 To Len(sDec)
sD = sD & Int((lCarry * 10 + Mid(sDec, i, 1)) / 2)
lCarry = (lCarry * 10 + Mid(sDec, i, 1)) Mod 2
Next i
If Not blInt Then
If Right(sD, Len(sD) - lPosDec + 1) <> _
String(Len(sD) - lPosDec + 1, "0") Then 'frac part is non-zero
i = Len(sD)
Do While Mid(sD, i, 1) = "0"
i = i - 1 'Skip trailing zeros
Loop
sD = Left(sD, lPosDec - 1) & Application.DecimalSeparator & _
Mid(sD, lPosDec, i - lPosDec + 1) 'Insert decimal point again
End If
End If
i = 1
Do While i < Len(sD)
If Mid(sD, i, 1) = "0" Then
i = i + 1
Else
Exit Do
End If
Loop
If Mid(sD, i, 1) = Application.DecimalSeparator Then
i = i - 1
End If
sbDivBy2 = Right(sD, Len(sD) - i + 1)
End Function
Programmcode sbBinNeg
Bitte den Haftungsausschluss im Impressum beachten.
Function sbBinNeg(sBin As String, _
Optional lBits As Long = 32) As String
'Negate sBin: take the 2's-complement, then add one
'(C) (P) by Bernd Plumhoff 18-Dec-2021 PB V0.4
Dim i As Long
Dim sB As String
If Len(sBin) > lBits Or sBin = "1" & String(lBits - 1, "0") Then
sbBinNeg = CVErr(xlErrValue)
Exit Function
End If
'Calculate 2's-complement
For i = Len(sBin) To 1 Step -1
Select Case Mid(sBin, i, 1)
Case "1"
sB = "0" & sB
Case "0"
sB = "1" & sB
Case Else
sbBinNeg = CVErr(xlErrValue)
Exit Function
End Select
Next i
sB = String(lBits - Len(sBin), "1") & sB
'Now add 1
i = lBits
Do While i > 0
If Mid(sB, i, 1) = "1" Then
Mid(sB, i, 1) = "0"
i = i - 1
Else
Mid(sB, i, 1) = "1"
i = 0
End If
Loop
'Finally strip leading zeros
i = InStr(sB, "1")
If i = 0 Then
sbBinNeg = "0"
Else
sbBinNeg = Right(sB, Len(sB) - i + 1)
End If
End Function
Programmcode sbDecAdd
Bitte den Haftungsausschluss im Impressum beachten.
Function sbDecAdd(sOne As String, sTwo As String) As String
'Sum up two positive string decimals.
'Source (EN): http://www.sulprobil.de/sbdec2bin_en/
'Source (DE): http://www.berndplumhoff.de/sbdec2bin_de/
'(C) (P) by Bernd Plumhoff 18-Dec-2021 PB V0.4
Dim lStrLen As Long
Dim s1 As String
Dim s2 As String
Dim sA As String
Dim sB As String
Dim sR As String
Dim d As Long
Dim lCarry As Long
Dim lPosDec1 As Long
Dim lPosDec2 As Long
Dim sF1 As String
Dim sF2 As String
lPosDec1 = InStr(sOne, Application.DecimalSeparator)
If lPosDec1 > 0 Then
s1 = Left(sOne, lPosDec1 - 1)
sF1 = Right(sOne, Len(sOne) - lPosDec1)
lPosDec1 = Len(sF1)
Else
s1 = sOne
sF1 = ""
End If
lPosDec2 = InStr(sTwo, Application.DecimalSeparator)
If lPosDec2 > 0 Then
s2 = Left(sTwo, lPosDec2 - 1)
sF2 = Right(sTwo, Len(sTwo) - lPosDec2)
lPosDec2 = Len(sF2)
Else
s2 = sTwo
sF2 = ""
End If
If lPosDec1 + lPosDec2 > 0 Then
If lPosDec1 > lPosDec2 Then
sF2 = sF2 & String(lPosDec1 - lPosDec2, "0")
Else
sF1 = sF1 & String(lPosDec2 - lPosDec1, "0")
lPosDec1 = lPosDec2
End If
sF1 = sbDecAdd(sF1, sF2) 'Add fractions as integer numbers
If Len(sF1) > lPosDec1 Then
lCarry = 1
sF1 = Right(sF1, lPosDec1)
Else
lCarry = 0
End If
Do While lPosDec1 > 0
If Mid(sF1, lPosDec1, 1) <> "0" Then
Exit Do
End If
lPosDec1 = lPosDec1 - 1
Loop
sF1 = Left(sF1, lPosDec1)
Else
lCarry = 0
End If
lStrLen = Len(s1)
If lStrLen < Len(s2) Then
lStrLen = Len(s2)
sA = String(lStrLen - Len(s1), "0") & s1
sB = s2
Else
sA = s1
sB = String(lStrLen - Len(s2), "0") & s2
End If
Do While lStrLen > 0
d = 0 + Mid(sA, lStrLen, 1) + Mid(sB, lStrLen, 1) + lCarry
If d > 9 Then
sR = (d - 10) & sR
lCarry = 1
Else
sR = d & sR
lCarry = 0
End If
lStrLen = lStrLen - 1
Loop
If lCarry > 0 Then
sR = lCarry & sR
End If
If lPosDec1 > 0 Then
sbDecAdd = sR & Application.DecimalSeparator & sF1
Else
sbDecAdd = sR
End If
End Function
Download
Bitte den Haftungsausschluss im Impressum beachten.
Dieser Artikel als PDF Dokument:
Plumhoff_Schule_des_Denkens_von_Pólya.pdf [194 KB PDF Datei, ohne jegliche Gewährleistung]